Quantum Information Science
Written by Quantum Study Club on 18.22Arif Nurhasan S.T.
(Alumni Institute Technology Telkom, Indonesia)
Arip Nurahman
Department of Physics
Faculty of Sciences and Mathematics, Indonesia University of Education
and
Follower Open Course Ware at Massachusetts Institute of Technology
Cambridge, USA
Department of Physics
http://web.mit.edu/physics/
http://ocw.mit.edu/OcwWeb/Physics/index.htm
&
Aeronautics and Astronautics Engineering
http://web.mit.edu/aeroastro/www/
http://ocw.mit.edu/OcwWeb/Aeronautics-and-Astronautics/index.htm


Staff
Prof. Issac Chuang
Prof. Peter Shor
MAS.865J / 6.443J / 8.371J
Quantum Information Science
Spring 2006

Course Highlights
Course Description
This is an advanced graduate course on quantum computation and quantum information, for which prior knowledge of quantum mechanics is required. Topics include quantum computation, advanced quantum error correction codes, fault tolerance, quantum algorithms beyond factoring, properties of quantum entanglement, and quantum protocols and communication complexity.
Syllabus
 Help support MIT OpenCourseWare by shopping at Amazon.com! MIT OpenCourseWare offers direct links to Amazon.com to purchase the books cited in this course. Click on the Amazon logo to the left of any citation and purchase the book from Amazon.com, and MIT OpenCourseWare will receive up to 10% of all purchases you make. Your support will enable MIT to continue offering open access to MIT courses. Help support MIT OpenCourseWare by shopping at Amazon.com! MIT OpenCourseWare offers direct links to Amazon.com to purchase the books cited in this course. Click on the Amazon logo to the left of any citation and purchase the book from Amazon.com, and MIT OpenCourseWare will receive up to 10% of all purchases you make. Your support will enable MIT to continue offering open access to MIT courses. |
Course Description
This advanced graduate course on quantum computation and quantum information assumes a prior knowledge of quantum mechanics. We will cover models of quantum computation, advanced quantum error correction codes, fault tolerance, quantum algorithms beyond factoring, properties of quantum entanglement, and quantum protocols and communication complexity.
Prerequisites
Quantum Computation, Fall 2003 (2.111/18.435J)
Assignments
Students will complete one problem set every two weeks during the first half of the course. In the remaining half of the course, each student will pursue an active area of research in the field of theoretical quantum computing. Students will use their results to prepare an American Physical Society style paper and formal presentation.
Textbook
 Nielsen, Michael A., and Isaac L. Chuang. Quantum Computation and Quantum Information. Cambridge, UK: Cambridge University Press, 2000. ISBN: 9780521635035.
Nielsen, Michael A., and Isaac L. Chuang. Quantum Computation and Quantum Information. Cambridge, UK: Cambridge University Press, 2000. ISBN: 9780521635035.
Grading Policy
| ACTIVITIES | PERCENTAGES |
|---|---|
| Homework (4 Problem Sets) | 40% |
| Project Presentation | 20% |
| Project Paper | 40% |
Lecture Notes
This section contains documents created from scanned original files, which are inaccessible to screen reader software. A "#" symbol is used to denote such documents.
The lecture notes for this course were scribed by the students and are used with their permission.
| SES # | TOPICS | Students |
|---|---|---|
| 1 | Quantum Operations; Operator Sum Representation; System-Environment Model (PDF)# | Kayla Jacobs |
| 2 | Quantum Error Correction - Criteria and Examples (PDF) | Jennifer Novosad |
| 3 | Calderbank Shor Steane Codes (PDF)# | Saikat Guha |
| 4 | Stabilizers; Stabilizer Quantum Codes (PDF)# | Kayla Jacobs |
| 5 | Topological Quantum Codes; Kitaev's Anyon Model (PDF)# | Igor Sylvester |
| 6 | Stabilizers II; Computing on Quantum Codes (PDF)# | Danial Lashkari |
| 7 | Concatenated Codes; The Threshold Theorem (PDF)# | Salman Abolfathe |
| 8 | Cluster State Quantum Computation (PDF)# | Kayla Jacobs |
| 9 | Measurement and Teleportation Based Quantum Computation (PDF)# | Kayla Jacobs |
| 10 | Adiabatic Quantum Computation (PDF) | Edward Platt |
| 11 | Quantum Algorithms on Graphs; Quantum Random Walks (PDF) | Isaac Kim |
| 12 | Quantum Algorithms: The Abelian Hidden Subgroup Problem; QFT Over Sn (PDF)# | Kayla Jacobs |
| 13 | The Nonabelian HSP; Hidden Dihedral Group; Positive and Negative Results (PDF)# | Igor Sylvestor |
| 14 | Channels I: Quantum Data Compression; Entanglement Concentration; Typical Subspaces (PDF)# | Stephen Jordan |
| 15 | Channels II: Holevo's Theorem; HSW Theorem; Entanglement Assisted Channel Capacity (PDF)# | Saikat Guha |
| 16 | Channels III: Quantum-Quantum Channels, Mother/Father Protocol; Distillable Entanglement (PDF)# | Kayla Jacobs |
| 17 | Entanglement as a Physical Resource (PDF)# | Igor Sylvestor |
| 18 | Quantum Protocols - Quantum Communication Complexity; Distributed Algorithms (PDF)# | Jennifer Novosad |
| 19 | Quantum Games (PDF)# | Kayla Jacobs |
| 20 | Quantum Cryptography (PDF) | Edward Platt |
| 21-22 | Project Meetings | |
| 23-26 | Project Presentations |
Assignments
Problem Set 1 (PDF)
Problem Set 2 (PDF)
Problem Set 3 (PDF)
Problem Set 4 (PDF)
Calendar
Instructors
C = Isaac Chuan
S = Peter Shor
H = Sean Hallgren, Guest Lecturer
| SES # | INSTRUCTORS | TOPICS | KEY DATES |
|---|---|---|---|
| 1 | C | Quantum Operations; Operator Sum Representation; System-Environment Model | Problem set 1 out |
| 2 | C | Quantum Error Correction - Criteria and Examples | |
| 3 | S | Calderbank Shor Steane Codes | |
| 4 | S | Stabilizers; Stabilizer Quantum Codes | Problem set 2 out Problem set 1 due |
| 5 | S | Topological Quantum Codes; Kitaev's Anyon Model | |
| 6 | C | Stabilizers II; Computing on Quantum Codes | |
| 7 | C | Concatenated Codes; The Threshold Theorem | Problem set 3 out Problem set 2 due |
| 8 | C | Cluster State Quantum Computation | |
| 9 | C | Measurement and Teleportation Based Quantum Computation | |
| 10 | C | Adiabatic Quantum Computation | |
| 11 | S | Quantum Algorithms on Graphs; Quantum Random Walks | Problem set 4 out Problem set 3 due |
| 12 | H | Quantum Algorithms: The Abelian Hidden Subgroup Problem; QFT Over Sn | |
| 13 | H | The Nonabelian HSP; Hidden Dihedral Group; Positive and Negative Results | |
| 14 | S | Channels I: Quantum Data Compression; Entanglement Concentration; Typical Subspaces | |
| 15 | S | Channels II: Holevo's Theorem; HSW Theorem; Entanglement Assisted Channel Capacity | Project forms out Problem set 4 due |
| 16 | S | Channels III: Quantum-Quantum Channels, Mother/Father Protocol; Distillable Entanglement | |
| 17 | C | Entanglement as a Physical Resource | |
| 18 | C | Quantum Protocols - Quantum Communication Complexity; Distributed Algorithms | Project forms due |
| 19 | C | Quantum Games | |
| 20 | C | Quantum Cryptography | |
| 21-22 | Project Meetings | ||
| 23-26 | Project Presentations |
Download Course Materials
MAS-865JSpring-2006.zip (ZIP - 5.96 MB)
Click the link above to start downloading this course.
Quantum information science
Quantum information science concerns information science that depends on quantum effects in physics. It includes theoretical issues in computational models as well as more experimental topics in quantum physics including what can and cannot be done with quantum information. The term quantum information theory is sometimes used, but it fails to encompass experimental research in the area.
Subfields include:
- Quantum computing, which deals on the one hand with the question how and whether one can build a quantum computer and on the other hand, searching algorithms that harness its power (see quantum algorithm)
- Quantum computational complexity
- Quantum cryptography and its generalization, quantum communication
- Quantum error correction
- Quantum communication complexity
- Quantum entanglement, as seen from an information-theoretic point of view
Quantum teleportation is one well-known quantum information processing operation which reliably transfers an unknown quantum state from one point to another distant point, destroying the original state in the process.
References
- Nielsen, M.A. and Chuang, I.L. Quantum computation and quantum information. Cambridge University Press, 2000.
External links
- Quantiki – quantum information science portal and wiki.
- Quantum Information Science Gateway from The Physics Community
- ERA-Pilot QIST WP1 European roadmap on Quantum Information Processing and Communication
- QIIC – Quantum Information, Imperial College London.
- QIP – Quantum Information Group, University of Leeds. The quantum information group at the University of Leeds is engaged in researching a wide spectrum of aspects of quantum information. This ranges from algorithms, quantum computation, to physical implementations of information processing and fundamental issues in quantum mechanics. Also contains some basic tutorials for the lay audience.
- CQIST Center for Quantum Information Science & Technology at the University of Southern California


is studied by many people & research groups at MIT.
We offer several weekly research seminars. Sign up here to join the QIP Seminar mailing list.
Learn about quantum information by enrolling in one of MIT's courses (both graduate and undergraduate).
Use our e-print and journal search interface on to keep abreast of current research.
In town for a visit? Try our resources for visiting MIT. Finally, let us know how to make this site more useful for you with our feedback form.
Special Lecture Series on Statistical Physics of Algorithms (or Belief Propagation and Beyond)
Michael (Misha) Chertkov (Theory Division, Los Alamos National Laboratory)
A Knowledge Integration Community in the Cambridge-MIT Institute.
Time: 4-5pm
Date and Room:
Sep 29 Mon 32-141
Oct 1 Wed 32-141
Oct 2 Thur 36-156
Oct 27 Mon 32-141
Oct 29 Wed 32-141
Oct 30 Thur 36-156
An Emerging Field of Interdisciplinary Research and Education in Science and Engineering
| NSF Workshop | · | October 28-29, 1999 | · | Arlington, Virginia |
 | National Science Foundation |
An Emerging Field of Interdisciplinary Research and Education in Science and Engineering
October 28-29, 1999
Arlington, Virginia
| C. H. Bennett | IBM |
| D. P. DiVincenzo | IBM |
| N. Gershenfeld | MIT |
| H. M. Gibbs | University of Arizona |
| H. J. Kimble | Caltech |
| J. Preskill | Caltech |
| U. V. Vazirani | UC/Berkeley |
| D. J. Wineland | NIST |
| C. Yao | Princeton University |
Any opinions, findings, conclusions, or recommendations expressed in this report are those of the participants, and do not necessarily represent the official views, opinions, or policy of the National Science Foundation.
PREFACE
EXECUTIVE SUMMARY
INTRODUCTION
BIRTH OF A NEW SCIENCE
Compressibility and Capacity
- Quantum Entanglement
- Quantum Key Distribution
- Models of Quantum Computation
- Quantum Complexity Classes
- Quantum Searching and Lower Bounds
- Quantum Communication Complexity
- Quantum Error-correcting Codes
- Fault-tolerant Quantum Computation
- Quantum Information Processing in AMO Physics
- Nuclear Magnetic Resonance and Quantum Computation
CHALLENGES AND OPPORTUNITIES
New Quantum Algorithms
- Quantum Simulation
- Complexity Theory
- Quantum Cryptography
- Complexity-based Cryptography
- Quantum Error Correction and Fault Tolerance
- Precision Measurement and Quantum Control
- Many-party Quantum Entanglement
- The Quantum — Classical Boundary
- Quantum Information and Fundamental Physics
- Quantum Information Processing with Atoms and Photons
- Quantum Information Processing in Condensed Matter
- Toward Scalable NMR quantum computation
QUANTUM INFORMATION, CURIOSITY, AND COMMUNITY
FOSTERING THE CONTINUED SUCCESS OF QUANTUM INFORMATION SCIENCE
THE ROLE OF NSF
AGENDA
QUANTUM INFORMATION SCIENCE WORKSHOP ATTENDEES
PREFACE
Quantum Information Science (QIS) is an emerging field with the potential to cause revolutionary advances in fields of science and engineering involving computation, communication, precision measurement, and fundamental quantum science. The roots of this field go back about twenty years, when pioneers such as Charles Bennett, Paul Benioff, Richard Feynman, and others began thinking about the implications of combining quantum mechanics with the classical Turing computing machine.
The field of QIS began an explosive growth in the early to mid 1990’s as a consequence of several simultaneous stimuli: Peter Shor demonstrated that a quantum computer could factor very large numbers super-efficiently. The semiconductor industry realized that the improvement of computers according to Moore’s law would all too soon reach the quantum limit, requiring radical changes in technology. Developments in the physical sciences produced trapped atomic ions, advanced optical cavities, quantum dots, and many other advances that made it possible to contemplate the construction of workable quantum logic devices. Furthermore, the need for secure communications drove the investigations of quantum communication schemes that would be tamper proof.
In the course of supporting leading-edge research, several divisions at NSF had been supporting QIS-related projects for some time. However, the growing excitement and opportunities in QIS called for a careful examination of the NSF’s role in this new field, particularly since QIS required fundamental research in many areas of science and technology to reach its potential. Furthermore, QIS represents an important scientific basis for other national programs involving the quantum world, such as the Nanoscience and Technology Program. Strong investments in QIS by defense agencies and by science agencies around the world also indicated the perceived importance of QIS.
In this context, Robert Eisenstein, Ruzena Bajcsy, and Eugene Wong, Assistant Directors for the NSF Directorates of Mathematical and Physical Sciences, Computer and Information Science and Engineering, and Engineering, respectively, formed the QIS Working Group to organize a workshop to further explore NSF’s role in this field. The Working Group then recruited the QIS Steering Committee, consisting of leaders of the QIS community. The Steering Committee then organized the QIS workshop, which took place in Arlington Virginia, October 28-29, 1999. It was attended by approximately 100 scientists and engineers from all related disciplines. The workshop itself was an extremely stimulating event, due in part to the presence of a large fraction of the international leaders in the field. As one person put it: you could raise almost any question in QIS, and the pioneer on that point would be there to address it.
The workshop comprised oral sessions, breakout sessions, and an evening town meeting, which included further contributions and much discussion. The agenda and a list of attendees are appended. After the meeting the Steering Committee, listed on the first page of the workshop report, assembled an overview of the field, and made several recommendations regarding the role of NSF in meeting the needs of the field. Logistics for the workshop itself were handled very capably by Denise Henry. The report was reformatted for NSF systems by Ramona Winkelbauer, while publishing services were provided by Kelly DuBose and the NSF Publishing and Information Dissemination Service. The report is now being distributed widely throughout the QIS community and among federal agencies. The QIS Working Group is optimistic that the NSF will be responsive to the recommendations of this report.
Note that the report does not contain references to the literature. This was a deliberate decision to make the report as generally accessible as possible, without the normal scholarly detail and bibliographic information. There are a number of web sites that contain both historical and current research information on the field of QIS. Those listed below will link with others:
http://www.QUBIT.ORG/
http://www.euroquantum.org/
http://theory.caltech.edu/~preskill/ph229/
Finally, we would like to express our deep gratitude to the Steering Committee for their service in organizing and writing the report on the NSF QIS workshop. The meeting was an exceptionally stimulating experience for those in attendance, and the report is as wise as it is compelling. We believe that this will be a significant event in the field of QIS.
NSF Quantum Information Science Working Group:
Joseph L. Dehmer, Physics Division, MPS
Michael J. Foster, Division of Experimental and Integrative Activities, CISE
Lawrence S. Goldberg, Division of Electrical and Communications Systems, ENG
John W. Lightbody, Jr., Physics Division, MPS
Arthur Sanderson, Division of Electrical and Communications Systems, ENG
Hollis H. Wickman, Division of Materials Research, MPS
EXECUTIVE SUMMARY
Quantum information science (QIS) is a new field of science and technology, combining and drawing on the disciplines of physical science, mathematics, computer science, and engineering. Its aim is to understand how certain fundamental laws of physics discovered earlier in this century can be harnessed to dramatically improve the acquisition, transmission, and processing of information. The exciting scientific opportunities offered by QIS are attracting the interest of a growing community of scientists and technologists, and are promoting unprecedented interactions across traditional disciplinary boundaries. Advances in QIS will become increasingly critical to our national competitiveness in information technology during the coming century.
The information technology revolution of the past several decades has been driven by steady advances in the miniaturization of electronic circuitry on silicon chips, allowing performance to double roughly every 18 months ("Moore’s law"). But in fewer than 20 years, this shrinkage will reach atomic dimensions, necessitating a new paradigm if progress is to continue at anything like the rate we have become used to. Accordingly, considerable thought and long-range planning are already being devoted to the challenges of designing and fabricating devices at the atomic scale and getting them to work reliably, a field broadly known as nanotechnology.
However, it has long been known that atoms and other tiny objects obey laws of quantum physics that in many respects defy common sense. For example, observing an atom disturbs its motion, while not observing it causes it to spread out and behave as if it were in several different places at the same time. Until about five years ago, such quantum effects have mostly been seen as a nuisance, causing small devices to be less reliable and more error-prone than their larger cousins.
What is new, and what makes QIS a single coherent field despite spanning several traditional disciplines, is the realization that quantum effects are not just a nuisance, but in fact can be exploited to perform important and otherwise impossible information-processing tasks. Already quantum effects have been used to create unbreakable codes, and a quantum computer, if one can be built in the future, could easily perform some computations that would take longer than the age of the universe on today’s supercomputers. The way in which quantum effects speed up computation is not a simple quantitative improvement, like solving a hard problem more quickly by using a faster processor or many processors working in parallel. Rather it is a qualitative improvement, like the improvement one gets from calculating with decimal instead of Roman numerals. For the first time, the physical form of information has a qualitative rather than merely a quantitative bearing on how efficiently the information can be processed, and the things that can be done with it.
For this reason, even aside from its technological implications, QIS is an intellectually exciting field, with far-reaching implications for the basic mathematical and physical sciences, both theoretical and experimental. It is already providing a wholly new language for describing how Nature works, and new ways of thinking about a wide variety of scientific and technical questions. As with any revolutionary scientific insight, the long-term implications cannot be clearly anticipated, but we are confident that they will be profound. We also expect that the emergence of QIS will have an extensive eventual impact on how science is taught at the college and secondary level, and will bring a deeper understanding of quantum physics to a broad segment of the lay public.
While the potential economic impact of QIS is enormous, so are the problems that must be overcome before new quantum technologies can come to fruition. These problems are broad and deep, encompassing theory, experiment, and engineering. It is important to build the foundations of QIS that will provide the tools to solve these problems and enable progress toward more specific technical goals.
The development of QIS faces special problems because of its long time horizon and its intrinsically interdisciplinary nature. Researchers in the field work at the margins of the traditional disciplines, and therefore sometimes find it difficult to attain funding or to advance their careers. The very best students are attracted by the excitement generated by QIS, but are uncertain how to pursue that interest within a conventional academic department. Most worrisome, the excellent young scientists who receive advanced degrees doing QIS research are often forced to leave the field because of a lack of stable funding to support their work, despite the manifest relevance of QIS to the long-term economic health of the nation.
The National Science Foundation can and should play the leading role in addressing these problems and in fostering the continued success of quantum information science. We therefore recommend that:
INTRODUCTION
Quantum physics, information theory, and computer science are among the crowning intellectual achievements of the past century. Now, as the twenty-first century dawns, a new synthesis of these themes is underway. The emerging discipline of quantum information science (QIS) is providing profound new insights into fundamental problems relating to both computation and physical science. The flourishing of this new field in the next century may guide the way to revolutionary advances in technology and in our understanding of the physical universe.
The basic mathematical principles of quantum theory, which govern all known physical systems found in Nature, were established nearly 75 years ago. It was recognized early on that these principles imply that information encoded in quantum systems has weird and counterintuitive properties, yet the systematic study of quantum information began surprisingly recently. The explosive recent development of quantum information science can be attributed to two essential converging factors. First, the deepening understanding of classical information, coding, cryptography, and computational complexity acquired in the preceding decades has laid foundations that are ripe for extension to the quantum realm. Second, the development of sophisticated new laboratory techniques has provided the essential tools for manipulating and monitoring the behavior of single quanta in atomic, electronic, and nuclear systems.
While today’s digital computers process classical information encoded in bits, a quantum computer processes information encoded in quantum bits, or qubits. A qubit is a quantum system that can exist in a coherent superposition of two distinguishable states, and can be entangled with other such systems. The two distinguishable states might be, for example, internal electronic states of an individual atom, polarization states of a single photon, or spin states of an atomic nucleus. Entanglement is a subtle quantum kind of correlation having no classical equivalent, and can be roughly described by saying that two systems are entangled when their joint state is more definite and less random than the state of either system by itself. Two obvious properties of classical information are that it can be read and copied without being disturbed, and that the state of a composite system can be fully specified by specifying the state of each of its parts. But information carried by a quantum system flouts such common-sense principles. Indeed, quantum information can be exploited to perform tasks that would be impossible or very difficult in a classical world.
For example:
- Today’s digital supercomputers would take billions of years to find the prime factors of a number that is a few hundred digits long, whereas large-scale quantum computers, if they can eventually be built, might perform that task in just seconds.
- A classical computer requires a time proportional to N to search for a particular item in a list of N items, whereas a quantum computer can perform the search in a time proportional to the square root of N.
- If quantum information rather than classical information is exchanged between processors, then the amount of communication required to perform certain distributed computing tasks can be drastically reduced.
- A quantum computer could efficiently and accurately simulate the evolution of quantum many-body systems and quantum field theories that cannot be simulated on classical computers without making unjustified approximations.
- If quantum information is exchanged, cryptographic protocols can be devised in which privacy is ensured by principles of fundamental physics. In contrast, the security of public-key cryptosystems that are currently in widespread use rests on the assumption that decrypting a message requires a time-consuming computation (such as prime factorization), an assumption that could prove unwarranted if large-scale quantum computers become available.
Of the recent theoretical discoveries concerning quantum information, one of the most important and unexpected is that noisy quantum devices (if not too noisy) can reliably store and process suitably encoded quantum states. Ordinarily, complex quantum states like those that arise during intermediate stages of a quantum computation are extraordinarily fragile. But if a logical qubit is encoded, not as a single physical qubit, but instead in the form of entanglement among several physical qubits, it becomes far more robust. The new quantum error-correcting codes and fault-tolerant methods will be an essential part of any future effort to create, maintain, and manipulate intricate many-qubit quantum states.
With ongoing technological improvements, quantum information processing of moderate complexity should soon be feasible in a variety of physical implementations. It is reasonable to hope that one such implementation will eventually enable a full-scale quantum computer, but not any time soon. The technology of quantum cryptography is more mature and much closer to commercial realization. We also anticipate that QIS research will have a substantial impact on other quantum technologies, such as nanoscale engineering and precision metrology. Irrespective of the long-term technological implications, new capabilities for quantum information processing will undoubtedly drive exciting new discoveries in basic science.
It can also be foreseen that the emergence of quantum information science will have an extensive impact on science education. Quantum mechanics is usually taught at the undergraduate and graduate levels as part of the standard physics and chemistry curriculum, but the emphasis is more on applications than on developing a solid comprehension of the subject’s strange and seductive foundations. A course in quantum information science, by contrast, creates the opportunity and motivation for the student to confront the bare foundations without distractions. Students of physics, chemistry, mathematics, computer science, and engineering have the necessary background to benefit from such a course at an early undergraduate level. With appropriate modifications, it could even be given in high school, providing a valuable introduction to one of the great scientific ideas of the twentieth century, and a compelling illustration of the dictum that the universe is stranger and simpler than we can imagine.
The potential of quantum information technology is starting to be recognized by commercial companies and the defense establishment. But for this potential to be properly fulfilled, stable long-term support aimed at foundational scientific issues will be sorely needed. In recognition of this need and the importance of the field, a major initiative in quantum information has been launched in Europe. In the US, the National Science Foundation can nurture the development of quantum information science far more effectively than more mission-oriented agencies, or profit-seeking companies.
Future advances in quantum information science will require the combined effort of people with expertise in a wide variety of disciplines, including mathematics, computer science and information theory, theoretical and experimental physics, chemistry, materials science, and engineering. This profoundly interdisciplinary character is one of the most exhilarating aspects of the field. NSF can accelerate progress by encouraging collaboration and interaction among workers with widely disparate training and expertise. Furthermore, progress in quantum information can be sustained only by a substantial inflow of new talent, so it is also especially important to promote interdisciplinary education that will enable students to contribute effectively to this emerging scientific enterprise.
BIRTH OF A NEW SCIENCE
Quantum information science has arisen in response to a variety of converging scientific challenges. One goal is to probe the foundations of the theory of computation. What limits are imposed on computation by the fundamental laws of physics, and how can computational power be enhanced by exploiting the structure of these laws? Another goal is to extend the theory of communication. What are the ultimate physical limits on the performance of a communication channel, and how might quantum phenomena be harnessed by new communication protocols? Yet another challenge is to understand and overcome the quantum effects that constrain how accurately we can monitor and manipulate physical systems. What new strategies can be devised to push back the frontier of quantum-limited measurements, or to control the behavior of intricate quantum systems?
While quantum information science is a broad and rapidly expanding field, there are a few underlying recurrent themes. The theory of classical information, computation, and communication developed extensively during the twentieth century. Though undeniably useful, this theory cannot fully characterize how information can be used and processed in the physical world — a quantum world. Some achievements of quantum information science can be described as generalizations or extensions of the classical theory that apply when information is represented as a quantum state rather than in terms of classical bits (Fig. 1).
What makes this quest intellectually compelling is that the results are so surprising. At first glance, quantum effects seem to compromise our efforts to store, transmit, and process information, because quantum states are highly unstable and cannot be observed without being disturbed. Indeed, as the components of integrated circuits continue to shrink toward the atomic scale, quantum phenomena will pose increasingly serious limitations on the performance of information processing hardware, and one important task of quantum information science will be to illuminate whether and how such obstacles can be overcome. But the great surprise is that the news about quantum effects is not all bad — far from it! The fragility of quantum information becomes a very positive feature when it is recognized that eavesdropping on a quantum communication channel necessarily leaves a detectable imprint, so that communicating with qubits provides better privacy than communicating with classical bits. Far more astonishing, the intrinsic complexity of quantum information ensures that quantum systems of modest size are endowed with truly vast computational power, so that a quantum computer acting on just hundreds of qubits is capable in principle of performing tasks that could never be performed by conventional digital computers.
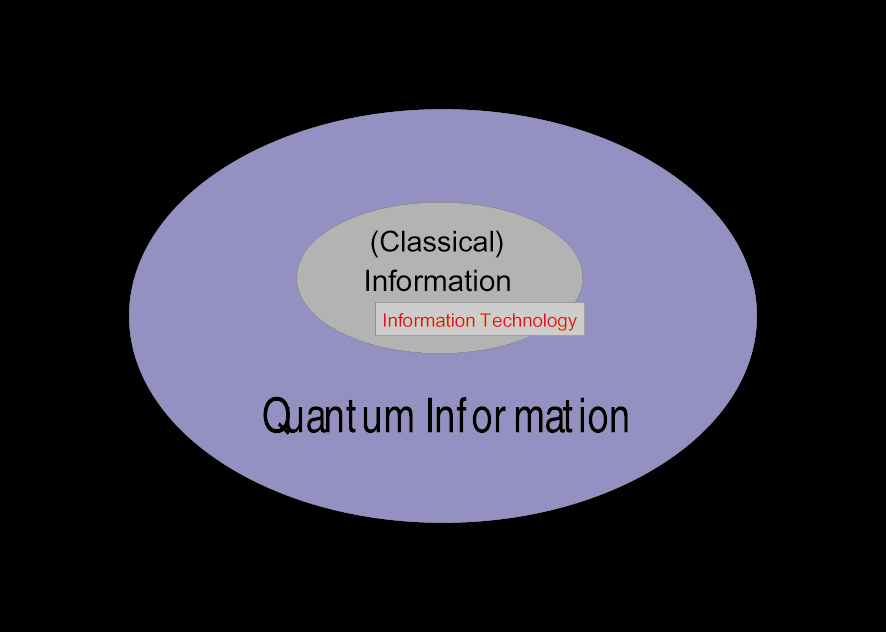
Figure 1: The well-established theory of classical information and computation is actually a subset of a much larger topic, the emerging theory of quantum information and computation.
Another recurrent theme is quantum entanglement, the non-classical correlations exhibited among the parts of a composite quantum system. A book expressed in classical bits can be read one page at a time. But if a typical "quantum book" were read one page at a time, hardly any of the information encoded in the book could be discerned. Instead, nearly all of the information resides in the correlations among the pages. This feature of quantum information, that it is typically encoded in the intricate correlations among the parts of a system, is the crucial way that quantum information differs from classical information, and underlies much of the magic of quantum computation and communication.
For example, while the number of bits of information encoded in a classical processor grows linearly with the size of the processor, the number of parameters needed to describe the state of a quantum processor grows exponentially with its size. The speedup achieved by quantum algorithms can be attributed to this separation in complexity between classical and quantum information, which arises because of the entanglement among the parts of a quantum system. Entanglement is also an essential feature of quantum error-correcting codes. These codes protect information by storing it in the correlations among the parts of the system; thus tearing a page from a suitably encoded quantum book does not destroy any encoded information, since that page by itself carries no information. Entanglement can also be viewed as a key resource that enables quantum communication protocols such as quantum teleportation, superdense coding, and quantum key distribution. A major goal of quantum information science is to characterize and quantify quantum entanglement, and to formulate new ways in which it can be exploited and manipulated.
A third recurrent theme is the laboratory manipulation of matter at the level of individual atoms or single quanta. Until recently, measurements of quantum systems were typically carried out on ensembles of many similarly prepared systems. Now, techniques for trapping and cooling atomic particles, and for nanofabrication of tiny electrical circuitry, are making it possible to monitor continuously the coherent interactions of an atom, photon, or electron. The information-theoretic approach to quantum dynamics provides an indispensable tool for understanding and controlling the behavior of these systems.
Let us briefly review some of the milestones already reached by quantum information science. Most have been achieved in just the past few years, and have generated a host of fascinating new questions.
Compressibility and Capacity
Classical information theory was launched by Claude Shannon, who discovered how to quantify the compressibility of a classical message, and how to characterize the capacity of a classical communication channel. The compressibility of a quantum message can also be quantified, and at least in the case where each letter of the message is a pure quantum state, the answer is closely analogous to that found by Shannon.
A quantum channel is one that conveys qubits rather than classical bits. The capacity of such a channel turns out to be a subtle concept, and a variety of important questions remain open. Several different types of channel capacity can be formulated and studied; in particular, it is important to distinguish between the amount of classical information and the amount of quantum information that can be reliably transmitted over a quantum channel. It has been shown that the classical capacity of a quantum channel can be enhanced if the communicating parties share a pre-existing entangled quantum state ("superdense coding"), and that the quantum capacity can be enhanced by two-way classical communication between the parties. One peculiar implication of the latter result is indicated in Fig. 2.
One of Shannon’s great insights was that a random code can reach the maximum achievable communication rate over a classical channel. A major surprise is that the corresponding statement does not apply for quantum channels — codes with a higher asymptotic rate than the random codes have been constructed.

Figure 2: A surprising property of the quantum channel capacity that illustrates a counterintuitive feature of quantum information. If a quantum channel is so noisy that it has no capacity to send quantum information, then using the channel twice in the same direction also sends not quantum information. But if the two transmissions are in opposite directions, the capacity is nonvanishing.
Quantum Entanglement
Quantum entanglement is a subtle nonlocal correlation among the parts of a quantum system that has no classical analog. Thus entanglement is best characterized and quantified as a feature of the system that cannot be created through local operations that act on the different parts separately, or by means of classical communication among the parts.
In the case of a pure quantum state of a system divided into two parts, the entanglement can be completely characterized because it can be reversibly converted to a standard currency. If many identical copies of a given state are available, then it is possible with local operations and classical communication to "distill" the entanglement into a standard form — many copies of a two-qubit Bell pair. And the Bell pairs, with local operations and classical communication, can be transformed back into many copies of the original state, with negligible losses. Thus the number of distillable Bell pairs provides a universal measure of bipartite pure state entanglement.
The situation is far more subtle and interesting for the case of entangled bipartite mixed states, or for pure-state entanglement with more than two parts. For example, some bipartite mixed states exhibit bound entanglement -- though entanglement is necessary to create these states, none of this entanglement can be distilled into Bell pairs. Another significant surprise is that even bipartite states with no entanglement can exhibit a peculiar kind of quantum nonlocality. One can construct a quantum book with two pages, such that it is impossible to read the book one page at a time, even though the two pages are not entangled with one another.
Since entanglement cannot be created locally, an entangled state shared by two widely separated parties can be a valuable resource (Fig. 3). One application of shared entanglement is a novel quantum communication protocol called quantum teleportation. If one party (Alice) possesses a qubit in an unknown state, she cannot observe the state without disturbing it. But if she shares a Bell pair with another party (Bob), then Alice can convey a perfect replica of her state to Bob by sending him just two bits of classical information. In the process, the shared Bell pair is consumed, and Alice’s original is destroyed. An odd feature of quantum teleportation is that the unknown state can take values in a continuum; nevertheless, thanks to the pre-existing shared entanglement, Bob needs to receive only two classical bits to recover the perfect replica. This protocol has been convincingly demonstrated in the laboratory.
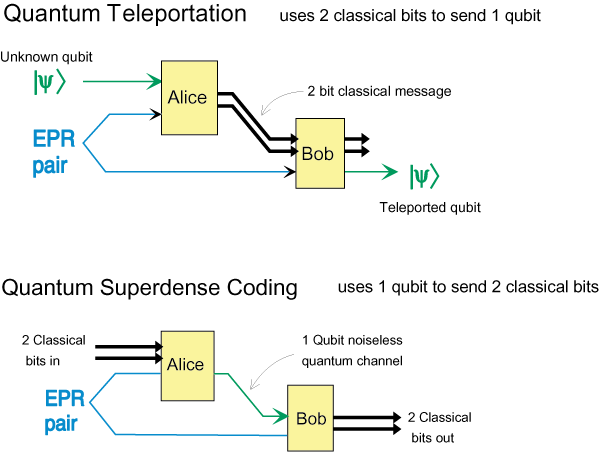
Figure 3: Two related tasks that require quantum entanglement as a resource. In quantum teleportation, Alice receives a qubit in an unknown state, and destroys it by performing a Bell measurement on that qubit and a member of an entangled pair of qubits that she shares with Bob. She sends a two-bit classical message (her measurement outcome) to Bob, who then performs a unitary transformation on his member of the pair to reconstruct a perfect replica of the unknown state. In superdense coding, Alice receives a two-bit classical message, transmits the message by performing a unitary transformation on a member of an entangled pair that she shares with Bob, and then sends that qubit to Bob. Thus one qubit suffices to carry two classical bits of information.
Quantum Key Distribution
Today’s protocols for secure Internet commerce depend on the presumed intractability of factoring large numbers, and would become insecure if fast factoring algorithms are discovered, or if large-scale quantum computations become practical. Although unconditionally secure encryption and authentication techniques do exist, they are used mainly in ultra-secure settings such as the Moscow-Washington hotline, because they depend on a resource that is difficult to provide in a commercial setting — a supply of truly random key information shared between the communicating parties but kept secret from everyone else. Quantum key distribution (QKD) provides a secure way of generating such key information.
Unlike other potential applications of quantum information science, quantum key distribution is practical with current technology, at least over moderate ranges such as tens of km of optical fiber, or ground-to-satellite optical links. Prototype QKD systems operating up to 48 km over conventional optical fiber, and 1 km through open air at ground level, are already functioning. An intermediate experimental goal for QIS research, easier than building a full-scale quantum computer, is the construction of quantum repeaters, which would make quantum key distribution feasible over arbitrarily large distances.
Quantum key distribution has recently been proved "unconditionally secure" against an adversary who eavesdrops on the quantum transmission in any way allowed by the laws of quantum mechanics, but only under idealized assumptions that do not yet correspond to existing practical implementations. In all likelihood this gap can be closed, by a combination of theory (strengthening the existing proofs to cover more realistic sources, in particular dim coherent states) and experiment (single-photon sources and improved detectors). While current QKD implementations have concentrated on demonstrating basic feasibility, future implementations will include a quantitative analysis of potential eavesdropping and the privacy amplification protocols used to defeat it, so as to optimize the rate of safe key generation for any given combination of source, channel, and detector.
Models of Quantum Computation
The classical theory of computational complexity is founded on the modern Church-Turing thesis, which asserts that any "reasonable" model of computation can be efficiently simulated on a probabilistic Turing machine (a universal computer with access to a random number generator). But as far as we know, simulation of an n-qubit quantum computer on a classical computer requires a computation time that grows exponentially in n. Thus, while the theorems of classical complexity theory will stand forever as mathematical truths, they do not accurately portray the computational power woven into the laws of Nature.
Rather, the computational model dictated by physical law is the quantum Turing machine, or the equivalent quantum circuit model; these models can efficiently and accurately simulate the evolution of any quantum system governed by interactions that are local in space and time. A quantum circuit consists of wires and gates, but where the wires carry qubits, and the gates are unitary transformations. A computer that can execute just one generic two-qubit gate is adequate to perform universal quantum computation -- it can approximate any unitary transformation acting on n qubits to any desired accuracy. In the quantum circuit model, it is also assumed that qubits can be initialized in a particular standard state and measured in a particular standard basis. The final output of a quantum computation is obtained by measuring the qubits. Because of the randomness of the quantum measurement procedure, typical quantum algorithms are not deterministic; there is a probability distribution of possible outputs. Such algorithms can nonetheless be very useful, if for example the output provides the correct solution to a hard problem with high probability, and the correctness of the solution can be easily verified.
Quantum Complexity Classes
A dramatic example of a hard problem that can be efficiently solved by a quantum computer is the problem of finding the prime factors of a large composite integer. Though there is no proof, it is widely believed that prime factorization is an intractable problem on a classical computer, and indeed the presumed intractability of this problem and related problems is the basis of much of modern cryptography. Thus, a large-scale quantum computer would be a highly valuable code-breaking tool.
So far, only a few such explicit examples are known of quantum algorithms that achieve superpolynomial speedups compared to the corresponding classical algorithms. Meanwhile, the broader task of erecting a new theory of computational complexity compatible with quantum mechanics is now well underway, though still far from complete. For example, the class of problems that are efficiently solvable on a quantum computer (denoted BQP, for "bounded error probability, quantum polynomial time") is known to be contained in the classical complexity class P#P; in particular, a quantum computer can be simulated on a classical computer with a memory of polynomial size.
The natural quantum analog of the NP class for classical computation is denoted BQNP ("bounded error probability, quantum nondeterministic polynomial"). A problem is in NP if a trial answer offered by a "witness" can be verified in a time that grows no faster than a polynomial of the size of the input to the problem. Similarly, a computational problem is in BQNP if its solution can be verified in polynomial time on a quantum computer, but where the "witness" is a quantum state. It has been shown that the ground state energy problem is BQNP complete — the problem is to decide whether a "local" Hamiltonian (a sum of Hermitian operators, each involving a constant number of qubits) has an eigenvalue smaller than a specified energy E. Thus any problem in BQNP can be reduced to an instance of the ground state energy problem after running for a polynomial time on a quantum computer. This result is the quantum analog of the Cook-Levin theorem, the centerpiece of classical complexity theory.
The study of interactive proofs, which combine randomness, non-determinism and interaction, has proved to be one of the most fruitful directions in classical computational complexity theory. A problem is in the class IP if a "prover" with great computational power can convince a "verifier" that he/she is able to solve the problem correctly. Recently quantum interactive proof systems have been defined and studied: a problem is in QIP if the prover can convince the verifier, but where now prover and verifier exchange qubits rather than classical bits. Quite surprisingly, it has been shown that one and one half rounds of quantum communication between prover and verifier are as powerful as many rounds of quantum communication.
Quantum Searching and Lower Bounds
Suppose that we are confronted by a very large unsorted database containing N items, and we are to locate one particular item. This search problem is particularly important, since it captures the essence of NP-hard problems such as satisfiability. A classical exhaustive search requires of order N steps to succeed with appreciable probability. But surprisingly, a quantum computer can perform the search in only of order N1/2 steps. The quantum search algorithm achieves a quadratic speedup relative to the classical search, in contrast to the superpolynomial speedup achieved by the quantum factoring algorithm, but quantum searching can be applied to a much broader spectrum of interesting problems.
Apart from devising new quantum algorithms that are faster than classical algorithms, it is also of great interest to obtain lower bounds on the resources needed by a quantum computer to solve a problem. In fact, for the database search problem, a tight lower bound has been found, so that the known quantum search algorithm is actually optimal — no faster solution is possible. Although quadratic quantum speedups can be attained for a wide variety of problems, some problems have been formulated for which it can be shown that no quantum speedup is possible at all.
Quantum Communication Complexity
The power of quantum computation arises from the exponentially-many hidden degrees of freedom in the state of an n-qubit system. Can these degrees of freedom be tapped for super-efficient communication? The answer to this question is actually quite subtle. On the one hand, it is known that at least n qubits must be transmitted to send a message that is n bits long. But on the other hand, there are certain specialized communication tasks for which qubits really do offer a substantial advantage.
For example, suppose that two parties each maintain a calendar with N entries, and they want to find a time when both are available for a meeting. In the worst case, they will need to exchange of order N bits of classical information in order to have a reasonable probability of successfully arranging their date. The same task can be performed by exchanging only of order N1/2 log N qubits of quantum information. Qubits offer a far more dramatic advantage for the problem of dealing hands containing N1/2 from a deck of N cards. Classically, of order N1/2 bits must be exchanged. But the same task can be performed, with a success probability 1-d, by exchanging only of order log N log(1/d) qubits.
Quantum Error-correcting Codes
One of the most surprising recent developments in quantum information science, and one of the most important, is the discovery that unknown quantum states, if properly encoded, can be protected from errors (Fig. 4). Since the complex states that arise at intermediate stages of a quantum computation are extraordinarily fragile, quantum error correction will be essential to prevent large scale quantum computers from crashing.
The state of a quantum computer can be viewed as a vector in an abstract space of very high dimension. On first acquaintance, it sounds strange that a vector that takes values in a continuum (in contrast to the discrete values assumed by a classical bit string) can be protected against damage. How will we know if the vector drifts slightly in an unexpected direction? The secret of quantum error correction is to encode a quantum state in a cleverly selected subspace of a larger vector space. Errors that move the vector in a direction perpendicular to the code subspace can easily be detected and reversed, while errors parallel to the code subspace cause trouble. But if the code subspace is carefully chosen, typical errors will have only a very small component along the code subspace, and encoded information will be well protected.

Figure 4: A simple quantum error-correcting code. A single qubit of quantum information can be encoded as a highly entangled state of five qubits. If one of the qubits is heavily damaged by an interaction with the environment, the encoded quantum state can still be recovered perfectly.
The principles of quantum error correction were discovered less than five years ago, and the subject has developed explosively. Many explicit examples of quantum error-correcting codes have now been constructed. Nearly all of these fit into a beautiful unifying framework: the code subspace can be characterized as a simultaneous eigenspace of all the generators of an abelian group, the code’s stabilizer group. "Good" codes have been shown to exist — the number of encoded qubits and the number of errors that can be corrected both scale linearly with the size of the code block.
Fault-tolerant Quantum Computation
The existence of abstract quantum-error correcting codes is not in itself sufficient to ensure that quantum information can be stored reliably. The difficulty is that recovery from error requires a complex quantum computation, and further errors will inevitably occur as we carry out the recovery operation. Furthermore, we want more than reliable storage, we want to be able to process quantum information accurately. We need to devise procedures for error recovery and computation that are sufficiently robust as to work effectively even if implemented imperfectly. In particular, errors tend to propagate from one qubit to another when the qubits interact through the operation of a quantum gate — our procedures must be designed to keep this error propagation under control.
In fact, such fault-tolerant procedures can be formulated for any of the stabilizer quantum codes. When these procedures are used, quantum error correction really does improve the precision of a quantum computation, provided that the quantum gates are sufficiently accurate, and the decoherence times are sufficiently long. Indeed, an accuracy threshold for quantum computation can be established: if the probability of error per quantum gate is below a critical value, then an arbitrarily long quantum computation can be completed with negligible probability of error. The length of the code block needed to ensure good accuracy grows only polylogarithmically with the size of the computation to be performed.
The discovery of fault-tolerant methods has greatly improved the prospects for unleashing the power of quantum computation in realizable devices. Moreover, the new methods ensure that very intricate quantum systems can in principle be accurately controlled, with broad potential implications for basic physical science and for technology.
Quantum Information Processing in AMO Physics
Atomic, molecular, and optical (AMO) physics has long been at the forefront of the manipulation and control of individual quantum systems, with particularly spectacular developments resulting from the trapping and cooling of single electrons, ions, and neutral atoms. These advances are now enabling realizations of conditional quantum dynamics at the single-quantum level that are suitable for the implementation of quantum logic.
Nonlinear optics has been extended into the domain of single atoms and photons, leading to a demonstration of a quantum phase gate in which one photon induces a conditional phase shift on another via their mutual interactions with an atom in an optical cavity. Single trapped atoms have been cooled to the zero point of motion, and a quantum gate has been implemented by conditionally exciting a single phonon in an ion trap.

Figure 5: Photograph of five beryllium ions in a lithographically fabricated RF trap. The separation between ions is approximately 10 microns.
Since these initial demonstrations, experiments with trapped ions have continued to yield impressive achievements in the coherent manipulation of quantum systems, including the deterministic generation of entanglement between two ions in a trap. Further experiments with RF micro-traps will be able to extend this exquisite control of both internal states and quantized ion motion to larger systems (Fig. 5).
Experiments with single atoms and photons in cavity quantum electrodynamics (cavity QED) have also attained remarkable success. Number states of the radiation field have been created and quantum non-demolition detection of single photons accomplished. By integrating the techniques of laser cooling and trapping with those of cavity QED, real-time trapping of individual atoms has been achieved. Atoms can be tracked with precision approaching the standard quantum limit, leading to a new form of atomic microscopy.
On the theoretical front, AMO physics has provided important models for the implementation of quantum information processing that bridge the gap between abstract quantum algorithms and real physical systems. These models have stimulated new experimental advances, and have led to more detailed understanding of the interplay between physical dynamics and quantum information. For example, new quantum error correction protocols have been developed that are adapted to the dominant decoherence mechanism in ion trap and cavity QED computers, including a protocol that protects against certain types of dissipative events to all orders in the error probability.
AMO physics has led the advances in modern quantum measurement science for twenty years, in part because the fundamental physical mechanisms associated with both coherent and dissipative processes can be well-understood theoretically and accessed with great technical power in the laboratory. Indeed, many experiments in AMO physics have reached and in some cases have exceeded the standard quantum limits associated with zero-point or vacuum fluctuations.
Nuclear Magnetic Resonance and Quantum Computation
NMR has an unusual place among the prospective approaches for manipulating quantum information. While there are significant challenges to scaling ensemble quantum computing to large systems, it has been used in experimental simulations of non-trivial quantum algorithms, and has led to practical applications of quantum computing.
In NMR quantum computation, qubits are stored in the orientation of nuclear spins, which have very long coherence times. Exchange coupling through bonds provides a coherent nonlinear interaction, and gates are implemented by using radio frequency pulses to modify the spin evolution. Although the bonds cannot be switched on and off, their influence can be controlled through the spectroscopic techniques of refocusing and decoupling, so that a desired effective Hamiltonian can be synthesized from a known one. The most distinctive feature of NMR quantum computing is that a qubit is stored, not in a single underlying degree of freedom, but in about 1022 redundant copies.
Since the Zeeman splitting between nuclear spin states is a tiny fraction of the thermal energy in room-temperature NMR systems, the quantum state of the spins is very highly mixed. It therefore comes as a surprise that coherent processing of pure quantum states can be faithfully simulated in these systems. Among the achievements attained using NMR are simulations of quantum computations that require fewer logical steps than their classical counterparts, quantum error correction protocols, and efficient simulations of other quantum systems. These successes have raised intriguing and fundamental questions about the power of quantum information processing with highly mixed states.
The interaction between NMR and quantum computing has been beneficial in both directions. The demonstration of universal computation in molecules has led the chemistry community to realize that viewing a molecule as an information-processing device provides an entirely new language with applications far from computation. For example, an important unsolved spectroscopic problem had been exchanging the product operator coefficients between remote spins, so that a sensitive species could be used to read out information from an important but less-sensitive one. This kind of exchange is needed for the studies of complex molecular structure and function that are the foundation of modern synthetic chemistry and drug design. Following the initial NMR experiments for quantum computing, it was shown that the spin exchange problem could be solved by writing it in terms of the logical SWAP operations that are a computational primitive. The experimental demonstration of this protocol promises to have widespread applications.
Efforts are underway to make NMR quantum computing technology less expensive and more accessible (Fig. 6).
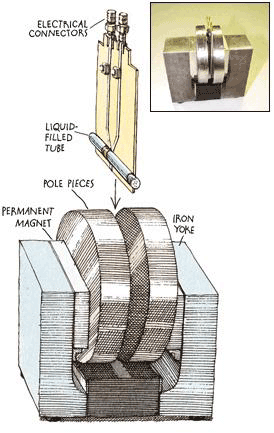
Figure 6: A "desktop quantum computer." Inexpensive table-top devices now under development, like the one sketched here, will be able to outperform the costly commercial NMR spectrometers that are used in current studies of room temperature ensemble quantum computation.
CHALLENGES AND OPPORTUNITIES
Quantum information science is a very new field, so new that many promising aspects of it have hardly been explored. Here we compile just a sampling of challenging open questions and problems.
Many of these unsolved problems span the traditional disciplinary boundaries. A common thread is the challenge of characterizing what can be achieved with quantum information processing, and how it can be achieved. We emphasize in particular that the physical requirements for quantum-state manipulation are entirely different from those for classical information processing; therefore it is essential that investigations of the potential physical implementations of quantum information processing be broad-based and exploratory.
New Quantum Algorithms
While the factoring and search algorithms are exciting breakthroughs that hint at the potential of quantum algorithms, our understanding of what quantum computers can do is still quite limited. It is very important to seek new quantum algorithms that can speed up the solutions to interesting problems.
The factoring algorithm makes use of a quantum Fourier transform that can be efficiently computed for any abelian group. The same ideas enable quantum computers to break a wide variety of cryptosystems. In fact, essentially all quantum algorithms that achieve exponential speedups fit into a common general framework: they find a hidden subgroup in an abelian group. Recent work shows that normal hidden subgroups in a non-abelian group can also be found efficiently. A major challenge is to extend this framework to the general non-abelian hidden subgroup problem.
Several problems seem to be excellent candidates to be solved by efficient quantum algorithms, but such algorithms have not yet been found. One example is graph isomorphism: given two graphs, can one be transformed to the other by a permutation of the vertices? Graph isomorphism can be expressed as a hidden subgroup problem in the symmetric group Sn. Other important examples are breaking the Ajtai-Dwork cryptosystem, which involves finding short vectors in certain types of lattices, and breaking cryptosystems based on classical linear error-correcting codes.
Quantum Simulation
In the long run, one of the most important applications of quantum computers is likely to be simulating the dynamics of quantum systems with many degrees of freedom. Much can be done to determine how quantum computers can best be used to address simulation problems of physical interest. Examples include the properties of quantum chromodynamics in real time or at finite nucleon density, or the behavior of quantum antiferromagnets and strongly correlated electron systems.
A particular challenge will be to determine if M-theory is susceptible to efficient simulation on a quantum computer. M-theory has been proposed as a unified description of all of the forces of Nature, including gravity. It can be formulated in terms of the quantum mechanics of very large matrices, but because of the intrinsic nonlocality of the theory, these matrices do not admit an obvious decomposition as a tensor product of smaller systems. It would be exciting to discover that no efficient simulation is possible, which would suggest that the computational power woven into the laws of Nature is even greater than we now suspect.
Quantum simulation may also play an important role in the evolution of new quantum technologies. Validating and characterizing the design of even relatively simple quantum devices will press the limits of conventional digital computing. In particular, a quantum computer would be an extremely valuable tool for the development of practical implementations of quantum feedback control.
Complexity Theory
The class of efficiently solvable problems on a quantum computer, BQP, is known to be contained in PSPACE, and is unlikely to contain NP. However, we do not yet know much about its relationship to other complexity classes. For example, is BQP contained in the polynomial hierarchy? In particular, does the power of approximate counting suffice to simulate quantum computation? There is evidence that BQP is not contained in MA (one-round interactive proofs), since there is an oracle relative to which the recursive Fourier sampling problem is not contained in MA.
The recent developments on the quantum analog of NP and quantum interactive proofs open up a number of fundamental issues. It should now be possible to classify a wide variety of problems about quantum systems as either being efficiently simulable on a quantum computer or BQNP-complete (much like the classification developed by the classical theory of NP-completeness). It is an open question to put the work on quantum interactive proofs in the framework of probabilistically checkable proofs, which is a deep and important part of computational complexity theory.
There are novel computational resources, other than time and space, that should be studied. One interesting question arises in the context of bulk NMR quantum computation with weakly polarized nuclear spins. Consider an n-spin system, which is described as a separable mixed state at every step in its evolution. Thus each instantaneous state is described by a probability distribution over orientations of n classical tops. However, if the evolution of the system is quantum mechanical (described by quantum gates), then it is not known whether such a system can be efficiently simulated on a classical computer, or whether it can simulate a universal quantum computation. Another intriguing question, which can also be posed in the context of bulk NMR quantum computation, is whether it is possible to carry out universal quantum computation if the initial state of the system is highly mixed. One recent result addresses the power of a quantum computer in which all qubits but one are initially in the uniformly mixed state. It was shown that if we restrict our attention to faithful simulations of a universal quantum computation, then such mixed state quantum computers are no more powerful than classical computers.
Apart from being important for a study of quantum computers, there are techniques of a fundamentally quantum nature that have provided new insights into classical complexity theory. Two examples are the linear lower bound on the communication complexity of the inner-product function and the reformulation of the log-rank conjecture for communication complexity. It is quite possible that the new method of quantum adversaries could provide an important new technique for classical computation as well.
Quantum Cryptography
Besides privacy and authentication, conventional cryptography includes other goals. For instance, a digital signature scheme allows Alice to send a message to Bob in such a way that Bob can verify that the message is really from Alice and that it has not been altered at all. A zero-knowledge proof allows Alice to prove to Bob that she knows how to solve a particular problem without Bob learning anything about how Alice’s solution works. One particularly intriguing example is "secure distributed computation," in which two or more cooperating parties evaluate a function of all of their inputs. Though some of the parties may be malicious or unreliable, the computation may nevertheless be reliable (the bad parties cannot alter the result) and discreet (the bad parties cannot learn any more about the others’ inputs than is implied by the value of the function).
There are classical solutions to these problems, but all rely on making some sort of assumption, such as a limitation on the computational power of a cheater. An important goal of QIS is to formulate quantum protocols that might allow us to weaken or remove these assumptions.
Many classical cryptographic protocols are built from simpler ("primitive") protocols. An important ‘primitive for two-party secure distributed computation’ is called bit commitment, the mathematical equivalent of Alice’s locking a bit in a safe and sending it to Bob. Bob cannot open the box until Alice gives him the key, but Alice cannot change her choice once she has given the box to Bob. It has recently been shown that unconditionally secure bit commitment is not allowed by the laws of quantum physics — if Alice and Bob have quantum computers, then whenever Bob is unable to determine the value of Alice’s bit, Alice can safely change her bit without Bob finding out. Still, it is of interest to develop two-party distributed computation schemes in which cheating is computationally difficult (though not absolutely impossible) with a quantum computer.
Complexity-based Cryptography
Since quantum computation compromises the security of much of classical cryptography, it is extremely important to develop a new cryptography that is immune to quantum cryptanalysis. For example, are there one-way functions that are easy for a quantum computer to evaluate, but hard for a quantum computer to invert? To design such primitives, we need to understand the limitations of quantum computation much better than we do today.
So far, three techniques have been developed for proving lower bounds on the running time of quantum algorithms: the hybrid argument, the method of polynomials, and the method of quantum adversaries. Extending this bag of tricks will better enable us to devise new cryptosystems that are invulnerable to a quantum attack.
It has been shown that any quantum algorithm for inverting a random permutation on N elements requires at least of order N1/2 steps. Since random permutations are regarded as good models for one-way functions, this result provides some positive evidence for the existence of one-way functions immune to quantum cryptanalysis. On the other hand, no non-trivial lower bound is known for the problem of finding a collision in a random 2-1 function. Since random 2-1 functions are regarded as good models for collision intractable hash functions (a fundamental cryptographic primitive), it is very important to understand the complexity of this problem.
Quantum Error Correction and Fault Tolerance
It is of great interest to refine the estimates of the accuracy threshold for quantum computation, as the threshold will define the specifications that must be met by the hardware components of a future quantum computer. Current estimates vary over a broad range, depending on assumptions about what protocol is used and how the noise is modeled; according to the most optimistic estimates, an error probability per gate as high as 10-3 can be tolerated. It is important to obtain more rigorous estimates that would apply to a broad spectrum of conceivable protocols.
It is also important to optimize the circuitry that implements the error recovery or the fault-tolerant quantum gates. Perhaps an even more promising approach to improving the threshold would be to investigate schemes for fault tolerance beyond the purview of the standard quantum circuit model. Drawing on analogies with classical error correction techniques will very likely be helpful.
Important computational efficiency considerations remain open. Current fault tolerant constructions require polylogarithmic overhead in time and in space. How much can these overhead requirements be reduced? In the classical case, constant overhead in time is sufficient, but it is not known whether this applies in the quantum case.
Also in need of further study are more general noise models. Much work on fault tolerance has focused on the problem of combating uncorrelated stochastic errors, but schemes that can overcome strongly-correlated noise should also be formulated and analyzed. More generally, there is a need to better understand how a quantum code can be devised that is well matched to the expected noise processes in a specific physical system.
Finally, new approaches to fault tolerance should be developed that achieve robustness through the design of the physical hardware. A particularly promising idea is to encode quantum information in the topological properties of the entanglement of many-body systems with local interactions. Topological quantum computation is a rich and promising subject, combining deep questions about topology, quantum error correction, and many-body quantum dynamics.
Precision Measurement and Quantum Control
Quantum information processing and quantum error correction will provide the laboratory scientist with unprecedented tools; these can be exploited to devise new strategies for performing interesting high-precision measurements.
An experimenter detects a time-dependent weak classical force by monitoring the response of a sensitive quantum system. But since observing the quantum system necessarily disturbs it, there are intrinsic limitations on the accuracy of the measurement. Quantum information theory has taught us that strategies that exploit entangled quantum states can collect more information than strategies that do not, so we can anticipate that the most precise measurement methods will require entangled probes (Fig. 7). Much work must be done to infer what resources are required to carry out a measurement of specified accuracy, and how best to deploy those resources under realistic laboratory conditions.

Figure 7: An example illustrating that, in a quantum setting, the best way to measure something can be a subtle issue. Two spins point along the same axis; they are parallel in case (a), anti-parallel in case (b). If the spins were measured one at a time, then the information collected about the spin axis would be the same in both cases. In fact, though, more information about the axis can be collect in case (b), because the optimal quantum measurement is an entangled measurement that acts on both spins at once.
Closely related to the challenge of high-precision measurement is the challenge of controlling quantum states. To control a system effectively, one needs to collect information about its behavior. Hence quantum control is particularly delicate — monitoring a system necessarily exerts back action on the system. Formulating effective protocols for quantum control poses daunting problems for both theorist and experimentalist.
Many-party Quantum Entanglement
The entanglement of a two-part pure quantum state can be conveniently quantified by the number of Bell pairs that can be distilled by local operations and classical communication. But it is still not known if it is possible to express the entanglement of a pure state with more than two parts in terms of some such standard currency. For example, it is unclear whether a three-party "cat" state should be regarded as possessing an entirely different kind of nonlocality than two-party Bell pairs.
A universal measure of many-particle pure-state entanglement, if one can be formulated, would have many applications. It might enable us to identify new kinds of quantum critical points at which the degree of entanglement of the ground state of a Hamiltonian changes discontinuously, or to characterize which kinds of quantum dynamics are hard to simulate on a classical computer.
The Quantum — Classical Boundary
A deep and long-standing fundamental problem is to understand and precisely define the transition from classical to quantum behavior. There are many systems in which quantum effects have a strength that depends on an adjustable parameter. It is usually easy to recognize the difference between a system that behaves very classically and one that behaves very "quantumly," but is there a sharp boundary between the two? And if so, where is the boundary? (Fig. 8)

Figure 8: The quantum--classical boundary. A classical computer can efficiently simulate a system that behaves classically, but not one that behaves "quantumly." Hence it is possible to identify a sharp transition between the quantum and classical phases of some physical systems.
Arguably, the most interesting observation ever made about the difference between quantum and classical is that a classical system cannot efficiently simulate a quantum system. We can try to use this idea to establish a well defined boundary between quantum and classical behavior. Indeed, the intrinsic accuracy threshold for quantum computation can be regarded as just such a phase boundary. Below the critical noise rate, there is long-range entanglement in the system, whereas above the threshold the entanglement between two subsystems decays exponentially as the subsystems are separated. The study of such transitions has barely begun, and there are many open questions. In particular, universality classes and critical exponents associated with long-range entanglement are yet to be identified.
Quantum Information and Fundamental Physics
The Standard Model of particle physics provides a marvelously accurate description of the fundamental constituents and their interactions down to distances of order 10-16 cm. But the most compelling fundamental questions concern physics at the Planck scale, 10-33 cm, where spacetime undergoes strong quantum fluctuations. While it seems hopeless to explore physics at these scales directly in high-energy accelerator experiments, a large-scale quantum computer might provide an incisive indirect probe of quantum gravity. At least one proposed model of physics at the Planck scale dictates that the dynamics of the universe actually can be efficiently simulated by a classical Turing machine. Since the factoring of numbers with of order 1000 digits is believed to be beyond the capability of any conceivable classical computer, a quantum computer of the future that achieves such a task will convincingly rule out any such model of Planckian physics!
Another possible way for quantum information science to illuminate the fundamental interactions is suggested by the discovery of fault-tolerant quantum computation. If quantum mechanics breaks down at very short distances, then we might say the "qubits" of the fundamental theory are continually subjected to errors — that is, to deviations from unitary evolution. Yet somehow, these errors are unseen at the larger distance scales we are currently capable of probing. How can it be so? Until quite recently, we lacked the tools to productively investigate this sort of question. But now hierarchical quantum error-correcting techniques have been found that exhibit this kind of behavior: the error rate gets smaller and smaller at higher and higher levels of the hierarchy. Could fault-tolerance be woven into the fundamental laws, so that the error rate flows to zero in the infrared limit? A broadening interface between quantum information science and fundamental physics can be anticipated, with tremendous potential payoffs.
Quantum Information Processing with Atoms and Photons
AMO physics provides powerful laboratory systems for the exploration of quantum information processing, quantum measurement, and quantum information dynamics. Because the relevant physical mechanisms and sources of dissipation can be understood and easily modeled, these systems are especially well suited for testing and developing error correction protocols. Existing experiments have achieved remarkable control of few-qubit systems. Extending this level of control to larger systems will require understanding and eliminating various sources of decoherence such as patch-effect fields and laser intensity and frequency fluctuations. But given the impressive rate of progress to date, it seems reasonable to anticipate that quantum information processing involving tens of qubits will be achieved within a decade.
Apart from their potential relevance to quantum computation and communication, the new capabilities arising from AMO physics will push the science of precision measurement into a radically new domain. Time-frequency standards, gravitational wave detection, and the characterization of solid state devices at low temperature are just a few of the frontiers of advanced metrology that will be affected.
Scaling
For quantum information processing to scale to increasing numbers of qubits, new experimental options must be explored to avoid a debilitating increase in technical overhead. One option in cavity QED is to move from more traditional Fabry-Perot cavities to nano-fabricated cavities in photonic bandgap materials. It might then be possible to trap and manipulate individual atoms by exploiting the powerful tools of lithography, while still maintaining strong coupling between individual atoms and single photons. A different option is to build an array of small traps, where atoms can be shuttled from one trap to another.
Quantum networks
One specific challenge is to combine the complimentary paradigms of flying and standing qubits in the construction of quantum networks for quantum communication and distributed quantum computation. As illustrated in Fig. 9, multiple atom-cavity systems located at spatially separated "nodes" could be linked via optical fibers to create a network of quantum information processors with quantum-coherent interconnects. A complete set of elementary network operations has been proposed and analyzed, including fault-tolerant local processing of quantum information, transmission of quantum states between nodes, and the distribution of quantum entanglement. If it could be realized, such a quantum Internet might support a wide range of quantum protocols.

Figure 9: Illustration of a protocol for the realization of a quantum network. An applied laser beam ( (t)) transfers quantum information from the internal state of an atom in one cavity to a photon state, via the atom-cavity coupling g. The photon travels along an optical fiber, enters a second cavity, and the information is transferred to an atom in that cavity. Nonlocal entanglement can be created among the atoms in the two cavities. By expanding from two cavities to a larger set interconnected by optical fiber, complex quantum networks can be realized.
(t)) transfers quantum information from the internal state of an atom in one cavity to a photon state, via the atom-cavity coupling g. The photon travels along an optical fiber, enters a second cavity, and the information is transferred to an atom in that cavity. Nonlocal entanglement can be created among the atoms in the two cavities. By expanding from two cavities to a larger set interconnected by optical fiber, complex quantum networks can be realized.
Optical lattices
Beyond ions traps and cavity QED, another system with promise for quantum information processing is an "optical lattice," in which neutral atoms are trapped by the AC-Stark shift produced by a set of intersecting laser beams. Because the atoms are neutral, they interact very weakly with the environment. Dissipation arising from inelastic photon scattering can be suppressed, as can other forms of dissipation such as coupling to phonons, defects, and impurities. Optical lattices have tremendous flexibility — a wide range of properties characterizing the lattice potential can be adjusted through laser beam geometry, polarization, intensity, and frequency. These adjustable "knobs" permit one to design interactions such that atoms interact strongly only during logic operations (e.g., via dipole-dipole interactions), but otherwise are isolated from each other and the environment. Substantial theoretical work needs to be done to assess the long-term potential of optical lattices as quantum information processing systems.
Quantum Information Processing in Condensed Matter
The ideas of quantum information processing are beginning to influence the agenda of condensed matter physics and materials science. A remarkable variety of proposed implementations of quantum bits and gates have been put forward, and their implications for experimental directions in these fields are being actively assessed by workers in the community.
Having been concerned for most of its history with bulk or collective properties, condensed matter physics is now beginning to address the behavior of systems where individual quantum properties are important. Qubits might conceivably be implemented in any of these systems, although so far only the rudiments of quantum gate operations have been achieved. The continuing quest for coherent information processing in a condensed matter setting will address some of the most fundamental problems in the quantum mechanics of individual systems.
Many specific quantum-gate technologies based on solid-state physics have been proposed. They include:
Ultra-small superconducting structures. In these, the qubit can be embodied either in the quantum state of flux of a SQUID (superconducting quantum interference device) or in the quantized Cooper-pair number of a small superconducting island. Single-qubit rotation has recently been observed (Fig. 10).

Figure 10: Quantum coherence in a superconducting Cooper-pair box. Cooper pairs of electrons can tunnel through the Josephson junction barrier onto the island electrode, and quantum information can be encoded in the number of Cooper pairs on the island. Coherent oscillations in the number of pairs were recently observed.
Quantum dots. Such structures have been the focus of nano-device technology both as optical and electronic devices. As quantum gates, their quantized electron number or spin can function as the qubit; switching of the quantum state might be achieved either by optical or electrical means.
Semiconductor optical microcavities. These devices, long researched for their applications in solid-state microlasers, are approaching the point at which the coherent manipulation of single photons is becoming a possibility. In addition, these can be coupled to atomic-like qubits in the form of embedded single-electron quantum dots. This proposal has many contacts with existing thrusts in optoelectronics.
Impurities in semiconductors. Integrated-circuit technology demands greater and greater control over the precise profile of dopant impurity concentrations in semiconductor devices. If this technology is developed to the extent that control of impurities atom-by-atom is achieved, quantum computation might become possible. The nuclear or electronic spins of individual phosphorus impurities are the qubits in this scheme, and transistors control operations between these qubits.
Various other systems, which are conceivable only because of the long development of science and technology in condensed-matter physics, have been proposed for implementing quantum computing devices — for example, using the orbital states of electrons floating on the surface of liquid helium, or the edge states of the quantum Hall effect. Undoubtedly, many other proposals will emerge as the workers in the various subfields of condensed-matter physics turn their imagination to the problem.
We envision a variety of specific ways in which quantum information science will influence the agenda of research in condensed-matter materials science in the coming years:
Phase coherence
The observation and characterization of quantum phase coherence has been a long-standing theme of mesoscopic physics; quantum computing gives a definite focus to this theme and asks new questions about how systems can be tailored to exhibit a high degree of coherence. In the superconducting community, the achievement of controlled single-qubit operations will be tantamount to achieving the long-standing goal of Macroscopic Quantum Coherence (MQC) in SQUIDs and related structures.
Entanglement
Some much-studied condensed matter systems, such as highly correlated electron systems and frustrated anti-ferromagnets, have very highly entangled many-body ground states, and the properties of the quasiparticle excitations of these systems reflect that underlying entanglement. But quantum entanglement among quasiparticles has had only a limited role in the description of solid-state phenomena, where single-particle descriptions have held the dominant place. (In certain subfields, such as in the optical physics of highly excited semiconductors, correlations among particles have received prominent attention.) New structures being proposed will result in the controlled generation of two-particle and eventually many-particle entanglement in a large variety of solid-state systems; this will require theory to explore how these various forms of entanglement can be characterized, and how well they can survive interaction with the various types of solid-state environments.
Readout
The "readout" requirements of quantum computing will provide additional impetus behind the drive to achieve high quantum efficiency measurements of, for example, single spins in solids; it will require the mastery of the subtle and counterintuitive issues of the quantum measurement problem, such as the construction of non-demolition measurements. Solid state researchers will have to travel the road now being explored in atomic physics, in which Schrödinger cat states are controllably created and undone, and measurements can be performed and then reversed again.
Fabrication and control
The structures that are proposed and that will be needed for this fundamental research will require a close encounter with state-of-the-art materials science and applied research in fabrication and in device physics. In a few of the proposals, individual dopant impurities in a semiconductor must be placed, one at a time, with unprecedented accuracy; new ion-beam or scanned probe deposition techniques will have to be developed to address this requirement. Some of the proposals for sensitive quantum measurement require the construction of magnetic-semiconducting heterostructures that have not been previously contemplated. The specifications of quantum gate operations put unprecedented demands on the bandwidth and precision of high-frequency gated control of microstructures. 1/f noise phenomena must be completely understood and suppressed in these structures. Many of these directions are ones that are already part of the agenda of advanced device technologies, but quantum computing probably pushes some of these technologies harder than any other computing schemes.
Communication
Quantum communications has engendered further thinking about how a solid state bit can be made mobile, and this has brought solid-state optics into the picture. Several proposals focus on the existence of various technologies, arising out of work on solid-state lasers, for the production of high quality-factor microcavities; it is known that quantum dots and other small quantum structures can be grown inside such cavities, and proposals for quantum gate operations, and for the transmission of a qubit as a photon emitted by the cavity, have been developed and will be the subject of future experimental research. Finally, there is even the possibility of using electrons themselves as mobile qubits; several proposals have been made for a Bell-type experiment, in which all steps — creation of entanglement, separation of the two particles, detection of the quantum states — are done electronically in a mesoscopic device.
Unorthodox implementations
Solid state physics is very versatile, and while the above survey can give some idea of how quantum information science and solid state physics may develop together in the future, it should not preclude an unforeseen departure from this "orthodox" view. For example, there is some discussion indicating that a recently identified gapped, fractional quantum Hall state (the " =5/2" state) may be the first "nonabelionic" state of matter, exhibiting quasiparticles with non-abelian, anyonic statistics. This discovery may actually have a real bearing on quantum information processing: calculations have indicated that nonabelionic matter may be uniquely suited as a medium for fault tolerant quantum computation. Will the
=5/2" state) may be the first "nonabelionic" state of matter, exhibiting quasiparticles with non-abelian, anyonic statistics. This discovery may actually have a real bearing on quantum information processing: calculations have indicated that nonabelionic matter may be uniquely suited as a medium for fault tolerant quantum computation. Will the  =5/2 state be the basis of a quantum computer? Probably not; but we should be open to possibilities like this, and to even more exotic-sounding ones.
=5/2 state be the basis of a quantum computer? Probably not; but we should be open to possibilities like this, and to even more exotic-sounding ones.
Toward Scalable NMR Quantum Computation
Many groups around the world are now using NMR to investigate small quantum computers, because of the familiarity and availability of the required spectrometers. A fundamental limitation will come in, however, beyond roughly 10 qubits. This is because room-temperature NMR uses a very weakly polarized sample, which leads to a partition function normalization that decreases exponentially as qubits are added. Although experimental refinements might reach the classical simulation limit of tens of qubits, it cannot scale beyond that. To go further, near-unity spin polarization is needed. Although this might be achieved by cooling the entire sample to millikelvin temperatures, that would eliminate the beneficial protection of intra-molecular coherence through translational thermalization. A more promising alternative is to cool just the nuclear spin system, which is routinely accomplished with optical pumping of rare-gas atoms. An open question is whether this will be possible with more complex molecules and in solids; if it is, the other parameters of this system are already close to what is needed for scaling to significant sizes.
It is important to view this scaling effort in the context of the complementary experimental approaches; as they progress they are all likely to grow together. Optical pumping for NMR draws on insights from AMO physics, and, in turn, NMR points to techniques for manipulating ensembles and effective Hamiltonians that are applicable to the alternatives. And the experimental progress in NMR to date has been driving the development of higher-level quantum programming tools that will be needed in any quantum computer.
QUANTUM INFORMATION, CURIOSITY, AND COMMUNITY
The development of conventional information technology has been neatly separated into physical scientists investigating underlying devices, and computer scientists working on architectures and applications. This division in both academia and industry has resulted in many of the most compelling questions about the meaning and manipulation of information being left neglected at the interface between hardware and software.
In contrast, one of the most striking features of the emerging science of quantum information is its transcendence of the division between abstract bits and physical quanta. To contribute in an arena where information content and physical embodiment are so intimately integrated, the early investigators needed mastery of many aspects of physics, computer science, engineering, and mathematics. An example that illustrates the symbiosis of computer science and physics is the successful adaptation of classical error correction ideas to quantum systems, an advance critical to the long-term viability of the field.
QIS has stimulated strong cross links between computation science and mathematical physics, and among areas such as AMO physics (e.g., NMR, cavity-QED, ion traps), condensed matter physics (e.g., electron/nuclear spins in semiconductors, single-electron transistors, coupled super-conducting systems), and engineering (e.g., nanotechnology, feedback, scalability, quantum-limited metrology). Direct evidence of these vibrant interfaces can be seen from the makeup of attendees at conferences and workshops on QIS.
Quantum information science is a field whose initial and future successes are clearly tied to its interdisciplinary nature. And, as is often the case in a scientific revolution, many researchers in QIS find themselves at the margins of their home disciplines, with their activities stretching the conventional limits of physics, computer science, mathematics, or electrical engineering. Indeed, a remarkable new generation of young researchers is growing up in an intellectual environment in which the traditional distinctions of discipline make less and less sense.
These developing cross links between diverse communities can be expected to directly benefit not only QIS, but science and technology more broadly, by catalyzing connections between various subfields of mathematics, physics, and engineering that might otherwise go unexplored. A principal benefit to industry is the cadre of young scientists and engineers who are being trained in new ways to help confront the challenges that lie beyond the end of VLSI scaling. For example, experimental investigations of possible physical implementations have nearly always been carried out in small laboratories, enabling students to be involved in all aspects of the research, from nano-fabrication to control theory to quantum algorithms.
Many of the best upcoming students are attracted to the study of quantum information because of its intellectual and technological impact. For them, QIS is not a specialized application to be encountered late in their education, but an organizing principle that drives an enormous appetite for learning about quantum systems and about the tools relevant for manipulating them. This ground swell among young people manifests itself in enormously over-subscribed new courses taught across disciplinary boundaries. Courses in QIS can be aimed at the early undergraduate level, enabling an education in physics and other technical fields to reach a broader and more enthusiastic audience.
The continuing investigation of the intimate connections between information and physical systems may also enhance the role of science in society. Numerous magazines and newspaper articles have already been published in response to the lay-person’s fascination with computers and quantum physics. As quantum mechanics and information science continue to meld, this broad interest in QIS will help to bring science to a growing portion of the populace.
FOSTERING THE CONTINUED SUCCESS OF QUANTUM INFORMATION SCIENCE
Quantum information science has emerged as one of the most exciting scientific developments of the past decade. As described in the preceding sections, initial advances in QIS have encompassed a broad and remarkable landscape, ranging from super-fast quantum algorithms for computation and communication to fault tolerant architectures for quantum computers to the realization of quantum gates for the physical implementation of quantum logic. Beyond contributions to fundamental knowledge, these advances in QIS are of great potential technological significance to our society as information processing and communication march inexorably into the quantum realm.
In attempting to understand how best to foster the continued success of QIS, one should recognize that the most spectacular advances in the field have largely sprung from individual "zealots" who ventured beyond the boundaries of traditional disciplines and who did so without dedicated support for their activities (and in some cases, with active discouragement). The QIS community is largely a self-organized group of otherwise independent researchers drawn together by the intellectual excitement and potential of the field, sharing a strong incentive to learn as much as possible across a broad front, since no one can say from where the next great discovery will emerge. Moreover, the tools forged on one front are as likely as not to be employed on another, whether in investigations of physical dynamics with intrinsic fault tolerance, of new quantum algorithms, or of the engineering of materials for the new quantum components.
The brief history of QIS points to the essential role of "small science" driven by individual investigators. It is very important to continue to foster the research of individuals, and to encourage interactions across the traditional boundaries in physics, computer science, and engineering. Significant advances have sprung from unexpected quarters in the past, and further surprises should be expected — not just the emergence of new research directions but also the appearance of talented new people working in the field.
These considerations argue for stable long-term support of multidisciplinary research carried out by investigators either individually or in small collaborations. In the current scheme of things, there is a dearth of support for scientists and engineers whose research is aimed at foundational issues. Moreover, there is a pressing need to overcome structural problems of "dislocation." That is, students who are interested in quantum information science cannot be sure in which department to pursue that interest. Having nonetheless succeeded, these young graduates face yet another hurdle in that universities are reluctant to hire faculty working in a new and less established area that is not well matched to the department structure in academia.
In the end, there is no simple and obvious strategy for best fostering the continued advancement of a new field as diverse and dynamic as QIS. For each prescription for success there are conflicts and contradictions. For example, on the experimental front, the "individual PI" model will become increasingly difficult to sustain since the technical requirements for most experiments in QIS continue to become ever more daunting. There is thus a tension between maintaining diversity in investigations of physical systems and pursuing such investigations at the cusp of technical capability. Certainly instrumentation programs to support technically intensive research in QIS are vital to success. But equally certain is that the demand will greatly exceed the supply of funding for such programs. In concert with the various government agencies, industrial research laboratories, and national laboratories, the community will have to devise new research strategies that, on the one hand, foster the contributions of individual PIs and, on the other hand, address the question of optimal resource utilization.
THE ROLE OF NSF
The NSF can meet the need for stable, long-term support aimed at laying the foundations for a new science in a way that more mission-oriented agencies cannot (and have not). Although arguably the most spectacular results in QIS to date relate to large-scale quantum computation for cryptanalysis, NSF programs should be much more broadly based and should emphasize the development of a whole new area of science. As highlighted in preceding sections, promising topics "beyond the Shor" include quantum metrology, quantum networks and communication, and quantum components at the nanoscale. We note that, while the US (via the NSA in particular) has taken the lead in the effort to develop a large-scale quantum computer, we lag far behind the European community in establishing collaborations and research programs directed toward the broader foundations of QIS.
Much work in QIS will be hard to fund through traditional mechanisms because it is speculative and far from mainstream activities. An important role for NSF is to encourage "far out ideas" in new areas and to sustain long-term support directed toward "hard problems." However, the cycle of peer review and the organization of programs tend to favor incremental progress in well established areas instead. Furthermore, in the emerging arena of QIS, the traditional discipline-based organization of education and research may not be appropriate. Thus meeting the needs of the QIS community poses special problems, and we do not pretend to know the answers. Central issues are that support for QIS research should be coordinated among the NSF divisions, and that advocacy for QIS at NSF should be vested in some tangible form — advocates are essential to provide institutional memory at NSF and to ensuring long-term stability.
We favor support directed toward individual investigators engaged in "small science," which we feel will be more productive than funding concentrated in large centers. However, we do not preclude the concept of centers altogether; the cost of infrastructure and the benefits of collaboration could lead to a persuasive case that a portion of funding should be directed to center support. Novel concepts may be effective, such as "virtual centers" that promote exchanges of students and post-doctoral scholars. NSF-sponsored workshops might also help to foster productive interdisciplinary collaborations.
Especially important is the development of the careers of young people. Although QIS attracts the very best students, it is difficult for these students to continue to advance their careers after graduate school. While in part this is an unavoidable situation in a rapidly developing new field, the NSF can play an indispensable role by providing funding opportunities to help establish and maintain young careers. These young people are a vital resource not only for QIS but for the nation, in view of the ever increasing impact of information technology on our society.
AGENDA
NSF Workshop on Quantum Information ScienceArlington Hilton, Gallery I
Day 1, October 28, 1999
Morning Session
8:30 – 9:00 NSF Welcome, Introduction
Overview talks
A. Ekert, Chair
9:00 – 9:35 C. Bennett, Overview of Quantum Information 9:35 – 10:10 U. Vazirani, Quantum and Classical Complexity 10:10 – 10:45 G. Brassard, Quantum Communication and Cryptography 10:45 – 11:00 Coffee break 11:00 – 11:35 J. Preskill, Future Directions of Quantum Information Science 11:35 – 12:10 J. Kimble, Physical Implementations of Quantum Logic 12:15 – 1:30 Lunch
Afternoon Session – Physical Systems
B. Whaley, Chair
1:45 – 2:15 D. Wineland, Trapped Ion Quantum Computation 2:15 – 2:45 Y. Maguire, Ensemble Quantum Computing via NMR 2:45 – 3:15 P. Zoller, Quantum Computing with Atoms 3:15 – 3:45 R. Hughes, Activities in Quantum Information Science at LANL 3:45 – 4:15 Coffee break 4:15 – 4:45 B. Kane, Semiconductor Spin Quantum Computing 4:45 – 5:15 Y. Nakamura, Quantum Bit in a Single-Cooper-Pair Box 5:15 – 5:45 S. Koch, Quantum Effects in Excitonic Systems
8:00 – 10:00 Town Meeting
J. Dehmer, M. Foster, L. Goldberg, Jack Lightbody, Art Sanderson, Hollis Wickman
NSF Representatives
Day 2, October 29, 1999
Morning Session
C. Caves, Chair
8:30 – 9:00 A. Ekert, European Activities in Quantum Information Science 9:00 – 9:30 H. Everitt, Other U.S. Agencies Activities in Quantum Information Science
Quantum Information and Algorithms
Group I – Quantum Algorithms for Computation and Communication, Leader: C. Bennett (with D. DiVincenzo as scribe) 9:30 – 10:00 D. Aharanov, Error Correction and Fault Tolerance 10:00 – 10:15 Coffee break 10:15– 10:45 A. Kitaev, Topological Quantum Computing 10:45– 11:15 D. DiVincenzo, Protecting Quantum States via Symmetrization 11:15– 11:45 S. Lloyd, Quantum Modeling 11:45 – 12:15 M. Freedman, Quantum Field Theories and Quantum Computing 12:30 – 1:45 Lunch 2:00 – 4:00 Afternoon Breakout
Group II – Quantum Information and the Physical Sciences, Leader: J. Preskill (with C. Hood as scribe)
Group III – Physical Implementations, Leader: J. Kimble (with N. Amer as scribe)
4:00 – 5:00 Joint session with feedback from breakout groups, including recommendations for workshop report
5:00 Adjourn
Quantum Information Science Workshop Attendees
| Name | Institution |
| Dorit Aharonov | UC/Berkeley |
| Nabil Amer | IBM/Yorktown |
| Ruzena Bajcsy | NSF |
| Charles Bennett | IBM/Yorktown |
| Joseph Bordogna | NSF |
| Jack Boudreaux | NIST |
| Giles Brassard | University of Montreal |
| Phil Bucksbaum | University of Michigan |
| Aubrey Bush | NSF |
| Denise Caldwell | NSF |
| Carlton Caves | University of New Mexico |
| Isaac Chuang | Stanford University |
| Charles Clark | NIST |
| Arnold Dahm | Case Western University |
| Frederica Darema | NSF |
| Pankaj Das | UC/SD |
| Richard de Millo | Bellcore |
| Joseph Dehmer | NSF |
| Dennis Deppe | University of Texas |
| David DiVincenzo | IBM/Yorktown |
| Mark Dykeman | Michigan State University |
| Joseph Eberly | University of Rochester |
| Robert Eisenstein | NSF |
| Artur Ekert | Oxford University |
| Stephen Elbert | NSF |
| Michael Evangelist | NSF |
| Henry Everitt | ARO |
| Amr Fahmy | Harvard Medical School |
| Yeshaiahu Fainman | UC/SD |
| Eugene Fan | DOD |
| Nancy Forbes | Litton TASC |
| Lance Fortnow | NEC Research Institute |
| Michael Foster | NSF |
| Michael Freedman | Microsoft Corporation |
| Don Gammon | Naval Research Laboratory |
| George Gamato | |
| Neil Gershenfeld | MIT |
| Hyatt Gibbs | University of Arizona |
| Gerald Gilbert | Mitre Corporation |
| Lawrence Goldberg | NSF |
| Jozef Gruska | Informatics |
| Sanjay Gupta | Virginia Tech |
| Timothy Havel | Harvard Medical School |
| Mark Heiligman | NSA |
| Peter Hendrickson | NRO |
| Richard Hilderbrandt | NSF |
| Murray Holland | University of Colorado |
| William Holton | North Carolina State University |
| Cristina Hood | Caltech |
| Richard Hughes | Los Alamos National Laboratory |
| Richard Isaacson | NSF |
| Poul Jessen | University of Arizona |
| Nick Jones | |
| Paul Julienne | NIST |
| Subhash Kak | Louisiana State University |
| Bruce Kane | University of Maryland |
| Boris Kayser | NSF |
| Galina Khitrova | University of Arizona |
| Jeff Kimble | Caltech |
| Christopher King | Northeastern University |
| Alexey Kitaev | Caltech |
| Tom Kitchens | DOE |
| Stefan Koch | University of Marburg |
| Marvin Kruger | NSA |
| Rudolph Krutar | North Carolina State University |
| Chun-Lim Lau | Booz-Allen & Hamilton Inc. |
| Jean-Pierre Leburton | University of Illinois/UC |
| Zachary Lemnios | |
| Paul Lett | NIST |
| Jack Lightbody | NSF |
| Seth Lloyd | MIT |
| Samuel Lomonaco | University of Maryland/BC |
| Yael Maguire | MIT |
| Stephen Mahoney | NSF |
| Pierpaolo Malinverni | European Commission |
| Edgar Martinez | DARPA |
| Keith Miller | DOD |
| Martin Morf | Stanford University |
| Yasunobu Nakamura | NEC Research Laboratories |
| Nasser Peyghambarian | University of Arizona |
| John Preskill | Caltech |
| Winston Roberts | NSF |
| Steven Rolston | NIST |
| Mary Beth Ruskai | University of Massachusetts/Lowell |
| John Salasin | DARPA |
| Arthur Sanderson | NSF |
| Barry Schneider | NSF |
| Keith Schwab | NSA/Caltech |
| Alexander Sergienko | Boston University |
| Francisco Serpa | |
| Louis Sica | Naval Research Laboratory |
| Karen Sollins | NSF |
| Duncan Steel | University of Michigan |
| Bruce Taggart | NSF |
| T.J. Tarn | Washington University |
| Yosef Gavriel Tirat-Gefen | |
| Nikzad Toomarian | |
| Umesh Vazirani | UC/Berkeley |
| Dan Ventura | Penn State University |
| Nolan Wallach | UC/SD |
| Ian Walmsley | University of Rochester |
| Richard Webb | University of Maryland |
| Tom Weber | NSF |
| Birgitta Whaley | UC/Berkeley |
| Hollis Wickman | NSF |
| Carl Williams | NIST |
| David Wineland | NIST |
| Andrew Yao | Princeton University |
| Zeke Zalcstein | NSF |
| Roger Ziemer | NSF |
| Peter Zoller | University of Innsbruck |
OMB Clearance Number: OMB-3145-0058
Publication Number: NSF-00-101

 | Posted in »
| Posted in »



















0 comments: Responses to “ Quantum Information Science ”